Bank Slopes to 45 degrees

Calculate the optimal aspect ratio of a line graph by banking the slopes to 45 degrees as suggested by W.S. Cleveland. This maximizes the ability to visually differentiate differences in slope. This function will calculate the optimal aspect ratio for a line plot using any of the methods described in Heer and Agrawala (2006). In their review of the methods they suggest using median absolute slope banking ('ms'), which produces aspect ratios which are generally the median of the various methods provided here.

Usage

bank_slopes(
  x,
  y,
  cull = FALSE,
  weight = NULL,
  method = c("ms", "as", "ao", "was"),
  ...
)

Arguments

x: x values
y: y values
cull: logical. Remove all slopes of 0 or Inf.
weight: No longer used, but kept for backwards compatibility.
method: One of 'ms' (Median Absolute Slope), 'as' (Average Absolute Slope), 'ao' (Average Absolute Orientation), or 'was' (Weighted Average Absolute Orientation).
...: No longer used, but kept for backwards compatibility.

Value

numeric The aspect ratio (x , y).

Methods

As written, all of these methods calculate the aspect ratio (x /y), but bank_slopes will return (y / x) to be compatible with link[ggplot2]{coord_fixed()}.

Median Absolute Slopes Banking

Let the aspect ratio be $\alpha = \frac{w}{h}$ then the median absolute slop banking is the $\alpha$ such that, $$ median \left| \frac{s_i}{\alpha} \right| = 1 $$

Let $R_z = z_{max} - z_{min}$ for $z = x, y$, and $M = median \| s_i \|$. Then, $$ \alpha = M \frac{R_x}{R_y} $$

Average Absolute Slope Banking

Let the aspect ratio be $\alpha = \frac{w}{h}$. then the mean absolute slope banking is the $\alpha$ such that, $$ mean \left| \frac{s_i}{\alpha} \right| = 1 $$

Average Absolute Orientation Banking

Rather than averaging the slopes themselves, this method averages the orientation (angle) of each segment, since perceived slope differences are more closely related to angle than to the raw ratio $dy/dx$. Let $s'_i = s_i R_x / R_y$ be the range-normalized slopes. Then $\alpha$ is chosen such that, $$ mean \left| \arctan \left( \frac{s'_i}{\alpha} \right) \right| = \frac{\pi}{4} $$ This has no closed-form solution and is found numerically with uniroot.

Weighted Average Absolute Orientation Banking

This is the weighted version of Average Absolute Orientation Banking from Heer and Agrawala (2006). Each segment's absolute orientation is weighted by its length in display space, so both the orientation and its weight depend on $\alpha$. With $s'_i$ as above and segment run $dx_i$, $\alpha$ is chosen such that, $$ \frac{\sum_i \left|\arctan(s'_i / \alpha)\right| dx_i \sqrt{1 + (s'_i / \alpha)^2}} {\sum_i dx_i \sqrt{1 + (s'_i / \alpha)^2}} = \frac{\pi}{4} $$ This has no closed-form solution and is found numerically with uniroot.

All of these methods consider the entirety of the data at once, so they accentuate local features and can obscure larger-scale trends. Heer and Agrawala (2006) address this with multi-scale banking, which uses spectral analysis to identify the frequency scales present in the data and banks each one separately; see bank_slopes_multiscale and bank_plot_multiscale.

References

Cleveland, W. S., M. E. McGill, and R. McGill. The Shape Parameter of a Two-Variable Graph. Journal of the American Statistical Association, 83:289-300, 1988

Heer, Jeffrey and Maneesh Agrawala, 2006. 'Multi-Scale Banking to 45' IEEE Transactions On Visualization And Computer Graphics.

Cleveland, W. S. 1993. 'A Model for Studying Display Methods of Statistical Graphs.' Journal of Computational and Statistical Graphics.

Cleveland, W. S. 1994. The Elements of Graphing Data, Revised Edition.

Examples

library("ggplot2")

# Use the classic sunspot data from Cleveland's original paper
x <- seq_along(sunspot.year)
y <- as.numeric(sunspot.year)
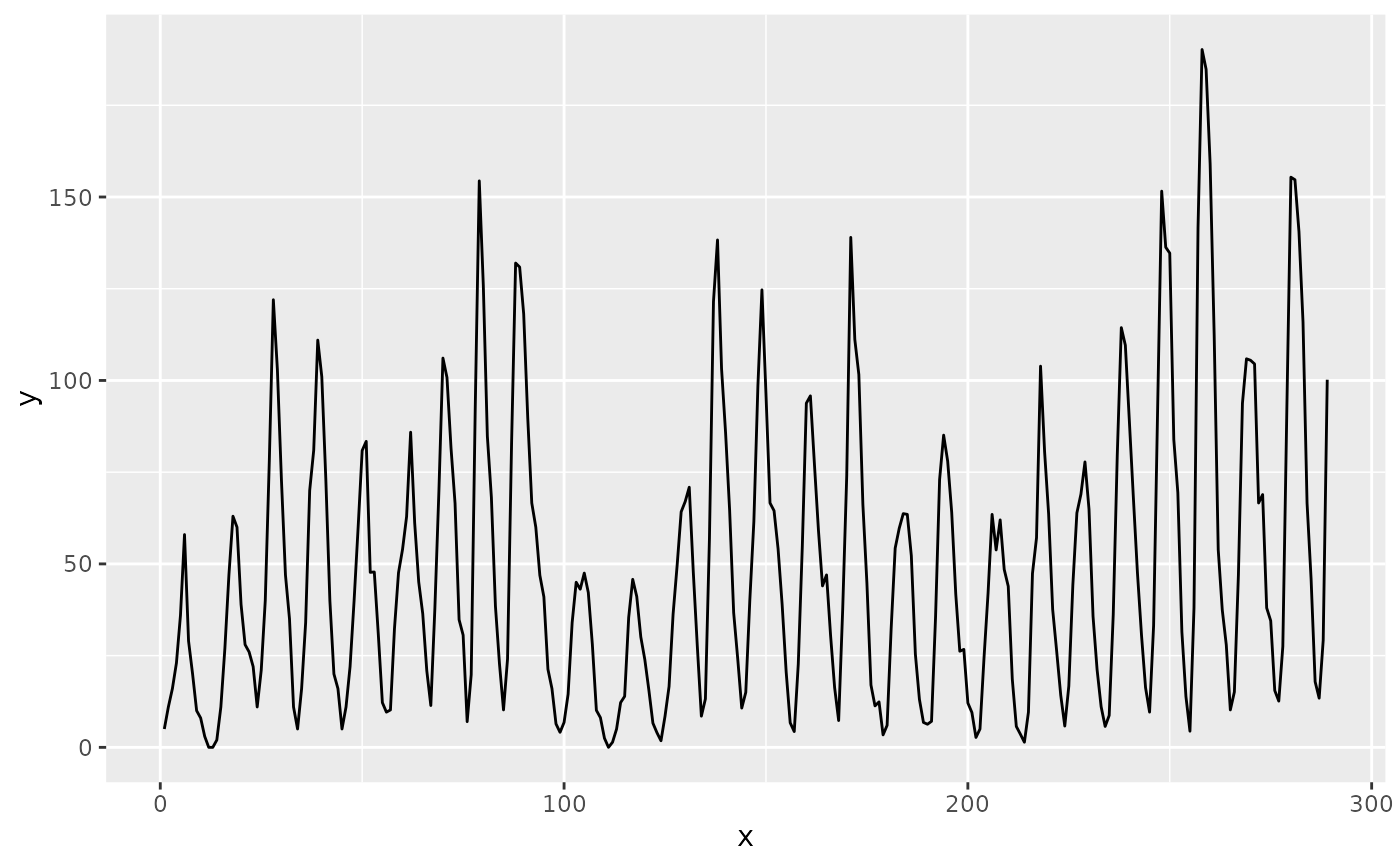
# Without banking
m <- ggplot(data.frame(x = x, y = y), aes(x = x, y = y)) +
  geom_line()
m


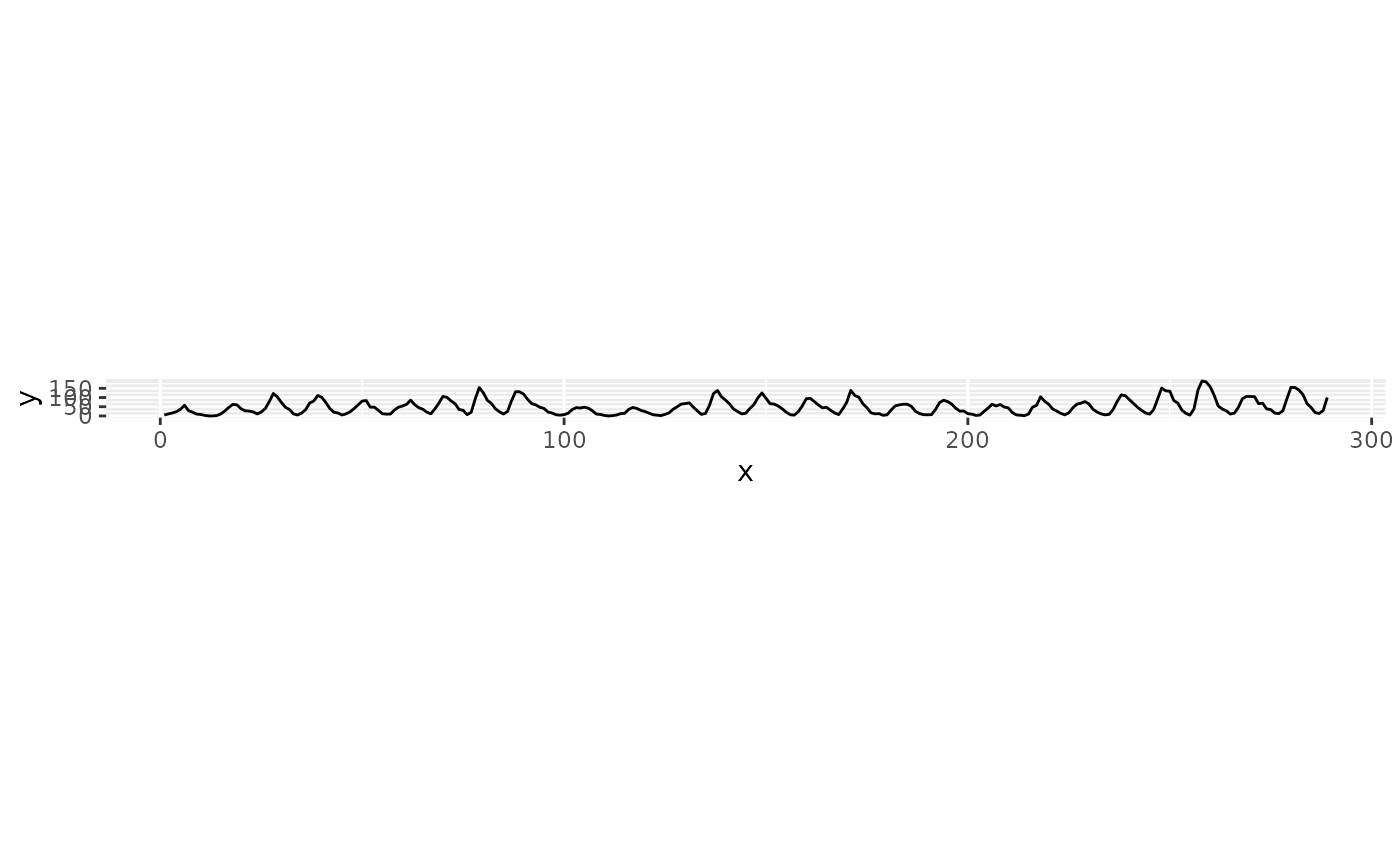
## Using the default method, Median Absolute Slope
ratio <- bank_slopes(x, y)
m + coord_fixed(ratio = ratio)


## Average Absolute Slope
m + coord_fixed(ratio = bank_slopes(x, y, method = "as"))


## Average Absolute Orientation
m + coord_fixed(ratio = bank_slopes(x, y, method = "ao"))


## Weighted Average Absolute Slope: each segment is weighted by its run in
## x, so this only differs from "as" when x is not evenly spaced
m + coord_fixed(ratio = bank_slopes(x, y, method = "was"))


## Culling removes slopes of 0 or Inf before banking, which matters when
## the data contains runs of repeated x or y values
bank_slopes(x, y, cull = TRUE)
#> [1] 0.04554598