10 Identification by fixing Legislator’s Signs
We can identify the scale and location of the latent dimensions by fixing the mean and location of the distribution of the legislator’s ideal points. This can be done by \[ \xi_i \sim \mathsf{Normal}(0, 1) \] This does not exactly fix the mean of \(\xi\) in any particular simulation. As the sample size increases, \(n \to \infty\) will give \(mean(\xi) \to 0\) and \(sd(\xi) \to 1\). This “soft-identification” will also overestimate the uncertainty in the ideal points of legislators (see paper by … ? ). So in the estimation, I do the following to ensure that in each simulation, \(\xi\) has exactly mean 0 and standard deviation 1. \[ \begin{aligned}[t] \xi_i^* &\sim \mathsf{Normal}(0, 1) \\ \xi_i &= \frac{\xi^*_i - \mathrm{mean}(\xi)}{\mathrm{sd}(\xi)} \end{aligned} \] However, this does not identify the direction of the latent variables. This can be done by restriction the sign of either a single legislator (\(\xi_i\)) or roll-call (\(\beta_i\)).
In this case, instead of fixing the \[ \beta_j \sim \mathsf{SkewNormal}(0, 2.5, d_j ) \] where \[ d_j = \begin{cases} -50 & \text{if Democratic party line vote} \\ 0 & \text{not a party line vote} \\ 50 & \text{if Republican party line vote} \end{cases} . \]
The skew-normal distribution is an extension of the normal distribution with an additional skewness parameter, \[ y \sim \mathsf{SkewNormal}(\mu, \sigma, \alpha) \] as \(|\alpha| \to \infty\), the skew-normal approaches a half-normal distribution.
map_df(c(-50, 0, 50),
function(alpha) {
tibble(x = seq(-4, 4, by = 0.1),
density = dsn(x, alpha = alpha),
alpha = alpha)
}) %>%
ggplot(aes(x = x, y = density, colour = factor(alpha))) +
geom_line()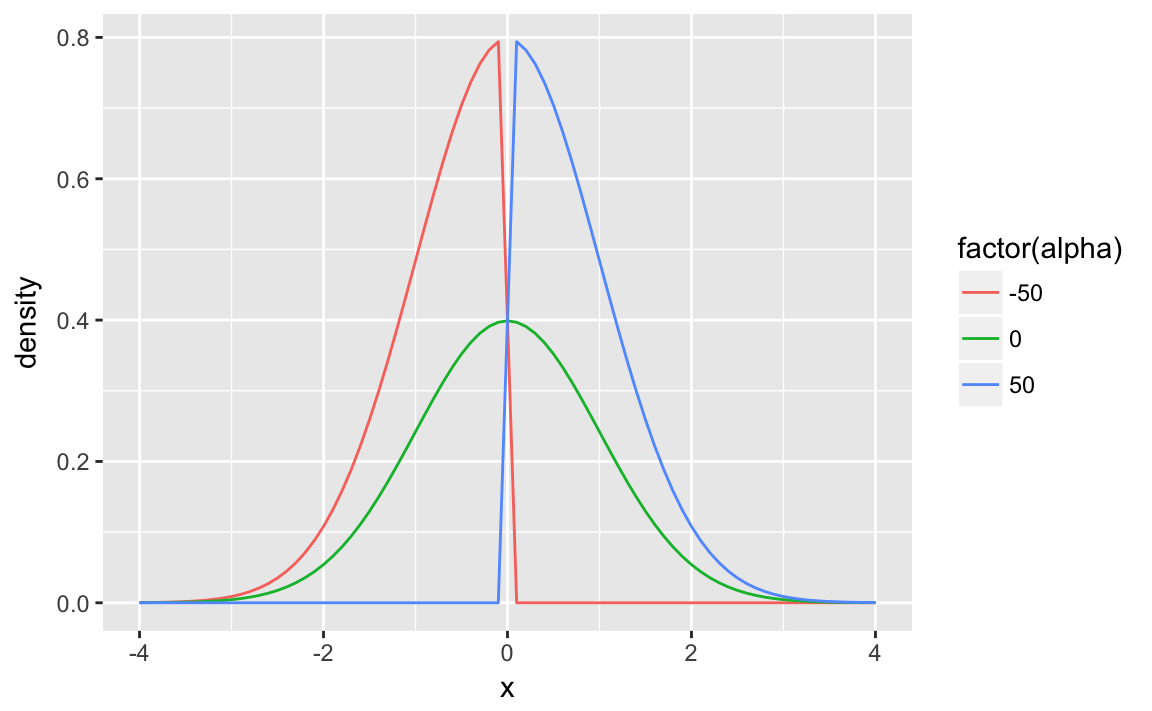
mod_ideal_point_3 <- stan_model("stan/ideal_point_3.stan")mod_ideal_point_3
// ideal point model
// identification:
// - ideal points ~ normal(0, 1)
// - signs of ideal points using skew normal
data {
// number of individuals
int N;
// number of items
int K;
// observed votes
int Y_obs;
int y_idx_leg[Y_obs];
int y_idx_vote[Y_obs];
int y[Y_obs];
// priors
// on items
real alpha_loc;
real alpha_scale;
real beta_loc;
real beta_scale;
// on ideal points
vector[N] xi_skew;
}
parameters {
// item difficulties
vector[K] alpha;
// item discrimination
vector[K] beta;
// unknown ideal points
vector[N] xi_raw;
}
transformed parameters {
// create xi from observed and parameter ideal points
vector[Y_obs] mu;
vector[N] xi;
xi = (xi_raw - mean(xi_raw)) ./ sd(xi_raw);
for (i in 1:Y_obs) {
mu[i] = alpha[y_idx_vote[i]] + beta[y_idx_vote[i]] * xi[y_idx_leg[i]];
}
}
model {
alpha ~ normal(alpha_loc, alpha_scale);
beta ~ normal(beta_loc, beta_scale);
// soft center ideal points
// in transformed block enforce hard-centering
xi_raw ~ skew_normal(0., 1., xi_skew);
y ~ bernoulli_logit(mu);
}
generated quantities {
vector[Y_obs] log_lik;
for (i in 1:Y_obs) {
log_lik[i] = bernoulli_logit_lpmf(y[i] | mu[i]);
}
}
Instead of fixing the ideal points, set the skewness parameter of the skew normal distribution so that \(\xi_{\text{FRIST (R TN)}} > 0\).
legislators_data_2 <-
within(list(), {
y <- as.integer(s109_votes$yea)
y_idx_leg <- as.integer(s109_votes$.legis_id)
y_idx_vote <- as.integer(s109_votes$.rollcall_id)
Y_obs <- length(y)
N <- max(s109_votes$.legis_id)
K <- max(s109_votes$.rollcall_id)
# priors
alpha_loc <- 0
alpha_scale <- 5
beta_loc <- 0
beta_scale <- 2.5
xi_skew <- if_else(s109_legis_data$legislator == "FRIST (R TN)", 50, 0)
})legislators_init_2 <- function(chain_id) {
list(xi_raw = if_else(s109_legis_data$party == "Republican", 1,
if_else(s109_legis_data$party == "Democratic", -1, 0)))
}legislators_fit_2 <- sampling(mod_ideal_point_3,
data = legislators_data_2,
init = legislators_init_2,
chains = 1, iter = 500,
pars = c("alpha", "beta", "xi"))